Qualche volta viene voglia di sapere da dove derivano le preziose indicazioni che si susseguono sul display del nostro computer sub, su cosa si basano i calcoli che esegue per offririrci quella sicurezza sulla quale contiamo.
Riferendoci alle consuete immersioni ad aria, tutto ruota intorno all’interpretazione ed alla valutazione dei meccanismi che regolano tempi e modi di assorbimento e liberazione del gas inerte, l’azoto, entrato in soluzione nel nostro organismo durante la permanenza ad una pressione maggiore di quella abituale.
Sappiamo (legge di Henry*) che nella vita quotidiana siamo in condizioni di saturazione alla pressione atmosferica di un bar, ossia dai nostri tessuti si liberano continuamente tante molecole di azoto quante ne entrano in soluzione con l’aria respirata.
Il coefficiente di sovrasaturazione è pertanto pari a 1 (C = 1).
In effetti è un equilibrio instabile a causa delle piccole, continue variazioni barometriche, ma si tratta di modificazioni irrilevanti e si può tranquillamente dire che la saturazione corrisponde alla nostra condizione di normalità. I tessuti sono di svariati tipi e per convenzione vengono suddivisi in compartimenti, distinguendoli in base alla velocità con cui assorbono il gas inerte. Schematicamente, possiamo suddividere i compartimenti in veloci, medi, lenti.
Andando sott’acqua per il breve spazio di tempo concesso da un’immersione con una bombola d’aria compressa, quel tranquillo stato di saturazione che ci è abituale viene stravolto. Ci si trova di fronte a situazioni in cui i compartimenti veloci hanno raggiunto sul fondo la saturazione alla pressione la esistente, i medi sono sotto saturi non essendo ancora a metà saturazione o avendola superata di poco, i lenti sono di solito lontanissimi anche da questo livello. Il problema è risalire senza che nessuno di essi, quando diventano più o meno sovrasaturi per la rapida diminuzione della pressione ambiente, liberi sotto forma di bolle l’azoto accumulato; o meglio, fare in modo che le inevitabili bolle siano contenute in numero e dimensioni, tali da non risultare pericolose nel loro vagare all’interno del circolo sanguigno. Haldane, lo scienziato che nei primi anni del 1900 inventò le tabelle di decompressione per regolare i tempi di risalita dei palombari, stabilì per tutti i tessuti un coefficiente di sovrasaturazione massimo di 1:2 (C = due), ossia asserì la loro capacità di sopportare il dimezzamento della pressione ambiente senza provocare incidenti causati da PDD (Patologia da decompressione). Da ciò deriva tra l’altro la possibilità teorica di rimanere in immersione a -10 m (2 bar) all’infinito, risalendo poi senza alcuna decompressione. I ricercatori moderni hanno potuto constatare che i tessuti veloci sono tali anche nel desaturarsi ed in più sopportano senza conseguenze tensioni di N2 ben maggiori di quanto ipotizzato da Haldane.
Il sangue ha un C = 3,1 e questo significa che per quanto lo riguarda si potrebbe restare un tempo illimitato a -21 m (3,1 bar) e tornare in superficie senza precauzioni. Per i lenti si è al contrario evidenziato che ci mettono una quantità di tempo a liberarsi del surplus di azoto e sopportano male una sovrasaturazione che superi il coefficiente 1,5. I medi hanno dimostrato comportamenti sensibilmente differenziati, tanto che sono poi stati suddivisi in medio-lenti e medio-veloci.
La realizzazione di un algoritmo, ossia di un modello sistematico di calcolo che dètti i parametri per una immersione ricreativa in sicurezza, è sempre impostato su questi presupposti, adattandone i parametri al livello di sicurezza che si vuole ottenere. Inoltre, i suoi calcoli di base prendono di solito in considerazione solo alcuni gruppi di tessuti, tralasciando quelli che non raggiungeranno mai condizioni di saturazione significative nel tipo di immersioni preventivate. Ecco spiegate le fondamentali differenze riscontrabili tra le tabelle di calcolo destinate ad una pesante attività lavorativa e le indicazioni dei computer finalizzati esclusivamente alle semplici immersioni ricreative.
Di ogni comparto si conosce il “periodo” ossia il suo tempo di emisaturazione, che corrisponde al tempo impiegato per giungere alla metà della saturazione, niente affatto uguale alla metà del tempo necessario per arrivare alla saturazione. Non si fa riferimento alla saturazione per il motivo che quest’ultima si completa solo in tempi lunghissimi e di non esatta determinazione. Lo dimostra la curva tendente all’infinito (detta quindi asintotica) che si ricava unendo I punti ricorrenti tra due assi cartesiani, sui quali sono riportate rispettivamente le percentuali di N2 assorbito ed il tempo durante il quale un tessuto è sottoposto ad una pressione. Ad ogni periodo o semiperiodo se si preferisce (tempo di emisaturazione) successivo al primo si ha una nuova emisaturazione, per cui: primo periodo uguale 50% della saturazione; secondo periodo uguale 75%; terzo periodo uguale 87,5%; quarto uguale 93,75; quinto uguale 96,87%; sesto uguale 98,43%; settimo uguale 99,21%, valore che si fa convenzionalmente corrispondere al massimo ottenibile. Anzi, in genere ci si ferma al sesto periodo.
Curva teorica dell’assorbimento di azoto da parte di un tessuto
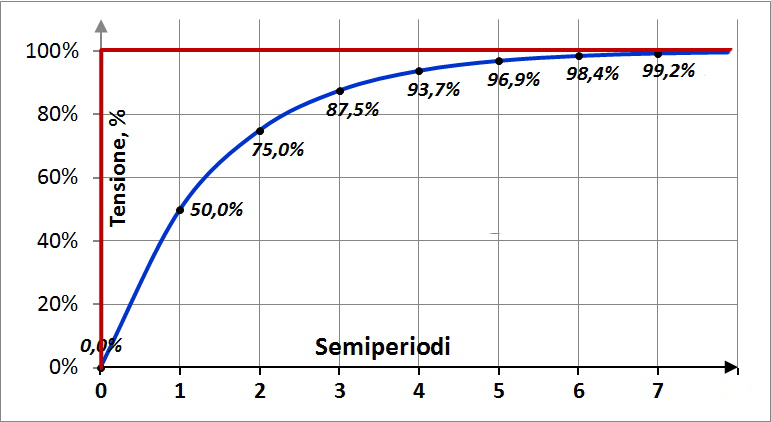
Il livello di saturazione corrisponde allora al tempo di immersione diviso il periodo, come risulta più chiaro dai seguenti esempi:
- In un’immersione di 70 minuti, un tessuto rapido con periodo di 10 minuti si satura in quanto 70 ÷ 10 = 7 periodi, quanti sono necessari per portare alla saturazione;
- Immersione di 50 minuti e tessuto medio con periodo di 60 minuti: 50 ÷ 60 = 0,83 periodi, ossia il tessuto non arriva nemmeno alla emisaturazione. Da tenere presente che il periodo resta invariato con l’aumentare della pressione.
Vediamo cosa succede al coefficiente C, ossia come cambiano i valori di saturazione nel corso di un’immersione come quella ora considerata e cosa cambia risalendo, presupponendo per quel tessuto un C/max = 1,8. Rimanendo per tutti i 50 minuti alla profondità di 25 m, al momento di inizio della risalita la saturazione, come visto sopra, sarà pari a 0,83 periodi, quindi al 41,5% (50’ x 0,83). Alla fine del primo periodo la tensione dell’azoto (pN2) raggiungerebbe la metà della sua pressione ambiente PN2 (0,79 x 3,5 bar x 0,50 = 1,38); poiché l’immersione ha una durata di 50’, inferiore al periodo del tessuto pari a 60’, avremo 1,38 x 0.83 = 1,14 (pN2 x periodo). La sovrasaturazione pari a 1,14 risulta inferiore al C/max (1,8) del tessuto in oggetto e per quanto lo riguarda non correremmo rischi da PDD nemmeno a seguito di una risalita di emergenza. Passando al comparto con periodo di 10’ visto sopra e assegnandogli un C/max = 2,6 controlliamo cosa succede in un’immersione ancora di 50 minuti alla quota di 25 m. La sua saturazione sarà pari a cinque periodi (50’ : periodo 10’) , cioè al 96,87%, con una pN2 di 0,79% per 3,5 bar a 25 m = 2,765 bar x 0,9687 (saturazione al quinto periodo) = 2,67 bar. Il coefficiente di saturazione (C = 1 al momento del tuffo) diventa 2,67 : 2,76 = 0,96 sul fondo, per passare a 3,37 (2,67 : 0,79) in superficie se si fosse costretti a tornare su veloci, con gravi rischi di incidente essendo oltre il limite di sovrasaturazione massima (C = 2,6) tollerabile da quel tessuto.
La desaturazione per rientrare nel C/max sopportato dal compartimento tissutale più esposto si ottiene, nelle solite immersioni ricreative, semplicemente rispettando la velocità prescritta di risalita, la quale ha il significato di una decompressione “in continuo”; superando determinati rapporti di tempo/profondità (la famosa curva di sicurezza) diventano necessarie le soste imposte dal computer. La complessità dei calcoli che sono alla base delle indicazioni dello strumento deriva dei tanti parametri di cui devono tenere conto, riferiti ciascuno ad ogni compartimento, le cui caratteristiche per giunta non sono esattamente definite e inalterabile. Soffermandosi sui conteggi relativi alla saturazione ed al variare dei coefficienti, ci si rende conto di quanto sia inesatta la convinzione che fa ritenere prive di rischi le lunghe permanenze in bassa profondità. Da queste, soprattutto se ripetute, deriva un pericoloso accrescersi di N2 nei compartimenti lenti, proprio quelli che spesso non sono contemplati dai computer dedicati alle immersioni ricreative. Immersioni superiori ai 90 minuti dovrebbero essere sempre evitate, cercando di non superare l’ora quando si va sott’acqua in modo intensivo come avviene di norma nei brevi soggiorni tropicali, dove certi fondali che non raggiungono i 15 m invitano a passeggiate senza fine. Per fortuna la scorta d’aria è limitata, ma immergersi tre volte al giorno per parecchi giorni di seguito porta inevitabilmente ad accumoli di azoto, per i quali potrebbero non essere sufficienti 24 ore di completa astensione iperbarica per tornare all’originario C = 1, auspicabile per prendere in tutta tranquillità l’aereo del ritorno. Comportamenti di questo genere tendono a fare uscire dai limiti di sicurezza inseriti nella metodologia decompressiva prevista, avvicinando a situazioni per le quali nel campo del lavoro subacqueo vengono adottate regole e prevenzione del tutto specifiche. La desaturazione dei tessuti lenti (I tempi più lunghi li richiedono le cartilagini, il cui periodo arriva a 635 minuti) è problematica e non sono sufficienti aggiustamenti empirici nella durata della decompressione per assicurarsi contro sgradite sorprese.

Luigi Fabbri
FUORI TESTO 1
* La legge di Henry - La qantità di gas che si scioglie in un liquido è direttamente proporzionale alla pressione del gas sul liquido e al tempo in cui si esercita la pressione, dipende dal tipo di gas e di liquido e diminuisce al crescere della temperatura.
L.F.
FUORI TESTO 2
Il coefficiente di saturazione è rappresentato dal rapporto tra la pressione parziale (pp) dell’azoto disciolto in un tessuto e la sua pressione parziale nell’aria respirata: C = pN2/pN2
In situazione normale a livello del mare si ha la saturazione poiché C = 0,79/0,79 = 1
Scendendo a -20 metri si è in stato di sottosaturazione poiché : 0,79/(0,79x3 bar) = 0,79 /2,37 = 0,33
Andando in montagna si è in sovrasaturazione: poniamo che il barometro indichi 0,7 bar:
C = 0,79/(0,7 x 0,79) = 0,79/0,55 = 1,43
L.F.




